I. Ο σκοπός και η σημασία της μέτρησης της σύγχρονης αυτεπαγωγής
(1) Σκοπός της μέτρησης των παραμέτρων της σύγχρονης επαγωγής (δηλαδή, της εγκάρσιας αξονικής επαγωγής)
Οι παράμετροι επαγωγής AC και DC είναι οι δύο πιο σημαντικές παράμετροι σε έναν σύγχρονο κινητήρα μόνιμου μαγνήτη. Η ακριβής λήψη τους είναι η προϋπόθεση και το θεμέλιο για τον υπολογισμό των χαρακτηριστικών του κινητήρα, τη δυναμική προσομοίωση και τον έλεγχο της ταχύτητας. Η σύγχρονη επαγωγή μπορεί να χρησιμοποιηθεί για τον υπολογισμό πολλών ιδιοτήτων σταθερής κατάστασης, όπως ο συντελεστής ισχύος, η απόδοση, η ροπή, το ρεύμα οπλισμού, η ισχύς και άλλες παράμετροι. Στο σύστημα ελέγχου κινητήρα μόνιμου μαγνήτη που χρησιμοποιεί διανυσματικό έλεγχο, οι παράμετροι του σύγχρονου επαγωγέα εμπλέκονται άμεσα στον αλγόριθμο ελέγχου και τα ερευνητικά αποτελέσματα δείχνουν ότι στην ασθενή μαγνητική περιοχή, η ανακρίβεια των παραμέτρων του κινητήρα μπορεί να οδηγήσει σε σημαντική μείωση της ροπής και της ισχύος. Αυτό δείχνει τη σημασία των παραμέτρων του σύγχρονου επαγωγέα.
(2) Προβλήματα που πρέπει να σημειωθούν κατά τη μέτρηση της σύγχρονης επαγωγής
Προκειμένου να επιτευχθεί υψηλή πυκνότητα ισχύος, η δομή των σύγχρονων κινητήρων μόνιμου μαγνήτη σχεδιάζεται συχνά ώστε να είναι πιο σύνθετη και το μαγνητικό κύκλωμα του κινητήρα είναι πιο κορεσμένο, με αποτέλεσμα η παράμετρος σύγχρονης επαγωγής του κινητήρα να μεταβάλλεται ανάλογα με τον κορεσμό του μαγνητικού κυκλώματος. Με άλλα λόγια, οι παράμετροι θα αλλάξουν με τις συνθήκες λειτουργίας του κινητήρα, με αποτέλεσμα οι ονομαστικές συνθήκες λειτουργίας των παραμέτρων σύγχρονης επαγωγής να μην μπορούν να αντικατοπτρίζουν με ακρίβεια τη φύση των παραμέτρων του κινητήρα. Επομένως, είναι απαραίτητο να μετρηθούν οι τιμές επαγωγής υπό διαφορετικές συνθήκες λειτουργίας.
2. μέθοδοι μέτρησης σύγχρονης αυτεπαγωγής κινητήρα μόνιμου μαγνήτη
Αυτή η εργασία συγκεντρώνει διάφορες μεθόδους μέτρησης της σύγχρονης επαγωγής και κάνει μια λεπτομερή σύγκριση και ανάλυση αυτών. Αυτές οι μέθοδοι μπορούν να κατηγοριοποιηθούν σε δύο κύριους τύπους: δοκιμή άμεσου φορτίου και έμμεση στατική δοκιμή. Η στατική δοκιμή διαιρείται περαιτέρω σε στατική δοκιμή AC και στατική δοκιμή DC. Σήμερα, το πρώτο μέρος των "Μεθόδων Δοκιμής Σύγχρονων Επαγωγέων" θα εξηγήσει τη μέθοδο δοκιμής φορτίου.
Η βιβλιογραφία [1] εισάγει την αρχή της μεθόδου άμεσου φορτίου. Οι κινητήρες μόνιμου μαγνήτη μπορούν συνήθως να αναλυθούν χρησιμοποιώντας τη θεωρία διπλής αντίδρασης για την ανάλυση της λειτουργίας φορτίου τους, και τα διαγράμματα φάσεων της λειτουργίας της γεννήτριας και του κινητήρα φαίνονται στο Σχήμα 1 παρακάτω. Η γωνία ισχύος θ της γεννήτριας είναι θετική με το E0 να υπερβαίνει το U, η γωνία συντελεστή ισχύος φ είναι θετική με το I να υπερβαίνει το U, και η εσωτερική γωνία συντελεστή ισχύος ψ είναι θετική με το E0 να υπερβαίνει το I. Η γωνία ισχύος θ του κινητήρα είναι θετική με το U να υπερβαίνει το E0, η γωνία συντελεστή ισχύος φ είναι θετική με το U να υπερβαίνει το I, και η εσωτερική γωνία συντελεστή ισχύος ψ είναι θετική με το I να υπερβαίνει το E0.
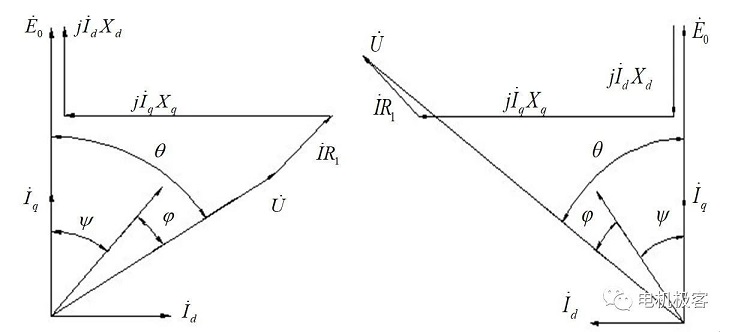
Σχήμα 1 Διάγραμμα φάσεων λειτουργίας σύγχρονου κινητήρα μόνιμου μαγνήτη
(α) Κατάσταση γεννήτριας (β) Κατάσταση κινητήρα
Σύμφωνα με αυτό το διάγραμμα φάσης, μπορεί να ληφθεί η εξής εξίσωση: όταν ο κινητήρας μόνιμου μαγνήτη λειτουργεί υπό φορτίο, μετράται η ηλεκτροκινητική δύναμη διέγερσης χωρίς φορτίο E0, η τάση ακροδέκτη οπλισμού U, το ρεύμα I, η γωνία συντελεστή ισχύος φ και η γωνία ισχύος θ και ούτω καθεξής. Μπορεί να ληφθεί το ρεύμα οπλισμού του ευθύγραμμου άξονα, η συνιστώσα εγκάρσιου άξονα Id = Isin (θ - φ) και Iq = Icos (θ - φ), τότε τα Xd και Xq μπορούν να ληφθούν από την ακόλουθη εξίσωση:
Όταν η γεννήτρια λειτουργεί:
Xd=[E0-Ucosθ-IR1cos(θ-φ)]/Id (1)
Xq=[Usinθ+IR1sin(θ-φ)]/Iq (2)
Όταν ο κινητήρας λειτουργεί:
Xd=[E0-Ucosθ+IR1cos(θ-φ)]/Id (3)
Xq=[Usinθ-IR1sin(θ-φ)]/Iq (4)
Οι παράμετροι σταθερής κατάστασης των σύγχρονων κινητήρων μόνιμου μαγνήτη αλλάζουν καθώς αλλάζουν οι συνθήκες λειτουργίας του κινητήρα και, όταν αλλάζει το ρεύμα οπλισμού, αλλάζουν τόσο το Xd όσο και το Xq. Επομένως, κατά τον προσδιορισμό των παραμέτρων, φροντίστε να αναφέρετε και τις συνθήκες λειτουργίας του κινητήρα. (Ποσότητα εναλλασσόμενου και συνεχούς ρεύματος άξονα ή ρεύματος στάτορα και εσωτερική γωνία συντελεστή ισχύος)
Η κύρια δυσκολία κατά τη μέτρηση των επαγωγικών παραμέτρων με τη μέθοδο άμεσου φορτίου έγκειται στη μέτρηση της γωνίας ισχύος θ. Όπως γνωρίζουμε, πρόκειται για τη διαφορά γωνίας φάσης μεταξύ της τάσης U του ακροδέκτη του κινητήρα και της ηλεκτροκινητικής δύναμης διέγερσης. Όταν ο κινητήρας λειτουργεί σταθερά, η τελική τάση μπορεί να ληφθεί απευθείας, αλλά η E0 δεν μπορεί να ληφθεί απευθείας, επομένως μπορεί να ληφθεί μόνο με έμμεση μέθοδο για να ληφθεί ένα περιοδικό σήμα με την ίδια συχνότητα με την E0 και μια σταθερή διαφορά φάσης για να αντικατασταθεί η E0, προκειμένου να γίνει μια σύγκριση φάσης με την τελική τάση.
Οι παραδοσιακές έμμεσες μέθοδοι είναι:
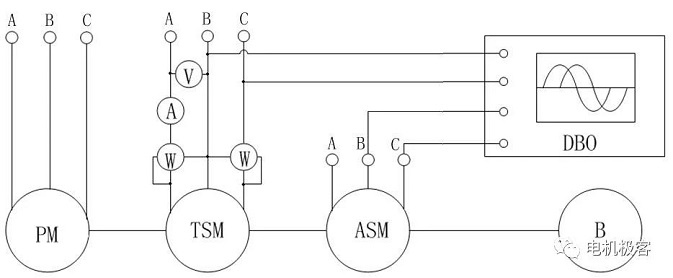
1) Στην υποδοχή οπλισμού του κινητήρα υπό δοκιμή, τοποθετήστε το βήμα και το αρχικό πηνίο του κινητήρα με αρκετές στροφές λεπτού σύρματος ως πηνίο μέτρησης, προκειμένου να επιτευχθεί η ίδια φάση με την περιέλιξη του κινητήρα υπό δοκιμή τάσης, συγκρίνοντας τη γωνία του συντελεστή ισχύος μέσω της σύγκρισης.
2) Εγκαταστήστε έναν σύγχρονο κινητήρα στον άξονα του υπό δοκιμή κινητήρα που είναι πανομοιότυπος με τον υπό δοκιμή κινητήρα. Η μέθοδος μέτρησης φάσης τάσης [2], η οποία θα περιγραφεί παρακάτω, βασίζεται σε αυτήν την αρχή. Το πειραματικό διάγραμμα σύνδεσης φαίνεται στο Σχήμα 2. Ο TSM είναι ο υπό δοκιμή σύγχρονος κινητήρας μόνιμου μαγνήτη, ο ASM είναι ένας πανομοιότυπος σύγχρονος κινητήρας που απαιτείται επιπλέον, ο PM είναι ο κύριος κινητήρας, ο οποίος μπορεί να είναι είτε σύγχρονος κινητήρας είτε κινητήρας συνεχούς ρεύματος, το B είναι το φρένο και το DBO είναι ένας παλμογράφος διπλής δέσμης. Οι φάσεις B και C του TSM και του ASM συνδέονται στον παλμογράφο. Όταν ο TSM συνδέεται σε τριφασική παροχή ρεύματος, ο παλμογράφος λαμβάνει τα σήματα VTSM και E0ASM. Επειδή οι δύο κινητήρες είναι πανομοιότυποι και περιστρέφονται συγχρόνως, το δυναμικό επιστροφής χωρίς φορτίο του TSM του δοκιμαστή και το δυναμικό επιστροφής χωρίς φορτίο του ASM, το οποίο λειτουργεί ως γεννήτρια, E0ASM, είναι σε φάση. Επομένως, μπορεί να μετρηθεί η γωνία ισχύος θ, δηλαδή η διαφορά φάσης μεταξύ VTSM και E0ASM.
Σχήμα 2 Πειραματικό διάγραμμα καλωδίωσης για τη μέτρηση της γωνίας ισχύος
Αυτή η μέθοδος δεν χρησιμοποιείται πολύ συχνά, κυρίως επειδή: ① στον άξονα του ρότορα τοποθετημένος μικρός σύγχρονος κινητήρας ή περιστροφικός μετασχηματιστής που απαιτείται για μέτρηση, ο κινητήρας έχει δύο άξονες τεντωμένα άκρα, κάτι που είναι συχνά δύσκολο να γίνει. ② Η ακρίβεια της μέτρησης της γωνίας ισχύος εξαρτάται σε μεγάλο βαθμό από την υψηλή αρμονική περιεκτικότητα του VTSM και του E0ASM, και εάν η αρμονική περιεκτικότητα είναι σχετικά μεγάλη, η ακρίβεια της μέτρησης θα μειωθεί.
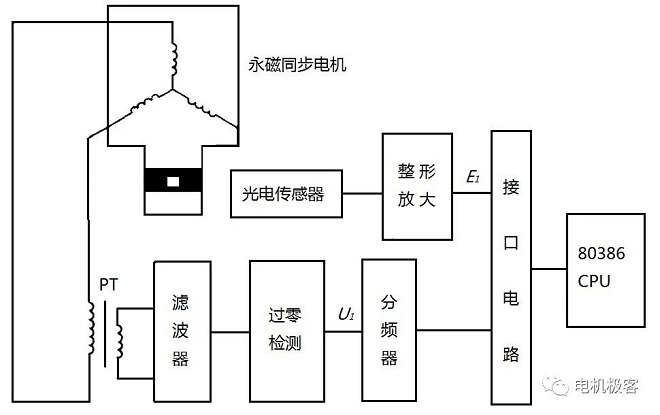
3) Για να βελτιωθεί η ακρίβεια της δοκιμής γωνίας ισχύος και η ευκολία χρήσης, τώρα χρησιμοποιείται περισσότερος αισθητήρας θέσης για την ανίχνευση του σήματος θέσης του ρότορα και στη συνέχεια η σύγκριση φάσης με την προσέγγιση τελικής τάσης
Η βασική αρχή είναι η εγκατάσταση ενός προβαλλόμενου ή ανακλώμενου φωτοηλεκτρικού δίσκου στον άξονα του μετρούμενου σύγχρονου κινητήρα μόνιμου μαγνήτη, ο αριθμός των ομοιόμορφα κατανεμημένων οπών στον δίσκο ή οι ασπρόμαυροι δείκτες και ο αριθμός των ζευγών πόλων του υπό δοκιμή σύγχρονου κινητήρα. Όταν ο δίσκος περιστρέφεται κατά μία περιστροφή με τον κινητήρα, ο φωτοηλεκτρικός αισθητήρας λαμβάνει σήματα θέσης ρότορα p και παράγει παλμούς χαμηλής τάσης p. Όταν ο κινητήρας λειτουργεί συγχρονισμένα, η συχνότητα αυτού του σήματος θέσης ρότορα είναι ίση με τη συχνότητα της τάσης του ακροδέκτη του οπλισμού και η φάση του αντανακλά τη φάση της ηλεκτροκινητικής δύναμης διέγερσης. Το σήμα παλμού συγχρονισμού ενισχύεται με διαμόρφωση, μετατόπιση φάσης και την τάση οπλισμού του κινητήρα δοκιμής για σύγκριση φάσης για να ληφθεί η διαφορά φάσης. Ορίστε όταν ο κινητήρας λειτουργεί χωρίς φορτίο, η διαφορά φάσης είναι θ1 (περίπου ότι αυτή τη στιγμή η γωνία ισχύος θ = 0), όταν το φορτίο λειτουργεί, η διαφορά φάσης είναι θ2, τότε η διαφορά φάσης θ2 - θ1 είναι η μετρούμενη τιμή γωνίας ισχύος φορτίου σύγχρονου κινητήρα μόνιμου μαγνήτη. Το σχηματικό διάγραμμα φαίνεται στο Σχήμα 3.
Σχήμα 3 Σχηματικό διάγραμμα μέτρησης γωνίας ισχύος
Όπως και στον φωτοηλεκτρικό δίσκο, ο ομοιόμορφα επικαλυμμένος με μαύρο και άσπρο σημάδι είναι πιο δύσκολος, και όταν οι μετρούμενοι πόλοι σύγχρονου κινητήρα μόνιμου μαγνήτη ταυτόχρονα δεν μπορούν να είναι κοινοί μεταξύ τους. Για λόγους απλότητας, μπορεί επίσης να δοκιμαστεί στον άξονα κίνησης του κινητήρα μόνιμου μαγνήτη τυλιγμένο σε έναν κύκλο μαύρης ταινίας, επικαλυμμένο με ένα λευκό σημάδι, η ανακλαστική πηγή φωτός του φωτοηλεκτρικού αισθητήρα που εκπέμπεται από το φως που συγκεντρώνεται σε αυτόν τον κύκλο στην επιφάνεια της ταινίας. Με αυτόν τον τρόπο, κάθε στροφή του κινητήρα, ο φωτοηλεκτρικός αισθητήρας στο φωτοευαίσθητο τρανζίστορ οφείλεται να λάβει ένα ανακλώμενο φως και αγωγιμότητα μία φορά, με αποτέλεσμα ένα ηλεκτρικό παλμικό σήμα, μετά την ενίσχυση και τη διαμόρφωση για να πάρει ένα σήμα σύγκρισης E1. Από το άκρο περιέλιξης του οπλισμού του κινητήρα δοκιμής οποιασδήποτε διφασικής τάσης, από τον μετασχηματιστή τάσης PT προς τα κάτω σε χαμηλή τάση, αποστέλλεται στον συγκριτή τάσης, σχηματίζοντας ένα αντιπροσωπευτικό ορθογώνιο φάσης του παλμικού σήματος τάσης U1. U1 από τη συχνότητα p-διαίρεσης, η σύγκριση του συγκριτή φάσης για να πάρει μια σύγκριση μεταξύ της φάσης και του συγκριτή φάσης. U1 από τη συχνότητα p-διαίρεσης, από τον συγκριτή φάσης για να συγκρίνει τη διαφορά φάσης του με το σήμα.
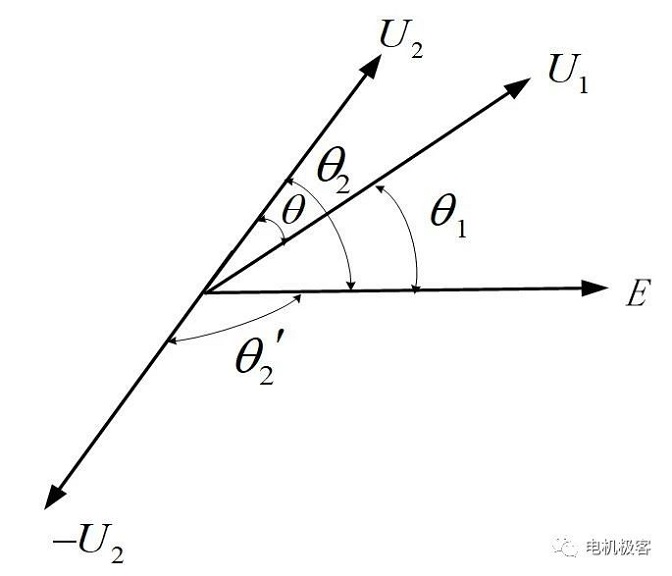
Το μειονέκτημα της παραπάνω μεθόδου μέτρησης γωνίας ισχύος είναι ότι πρέπει να γίνει η διαφορά μεταξύ των δύο μετρήσεων για να ληφθεί η γωνία ισχύος. Προκειμένου να αποφευχθεί η αφαίρεση των δύο μεγεθών και η μείωση της ακρίβειας, στη μέτρηση της διαφοράς φάσης φορτίου θ2, η αντιστροφή του σήματος U2, η μετρούμενη διαφορά φάσης είναι θ2'=180° - θ2, η γωνία ισχύος θ=180° - (θ1 + θ2'), η οποία μετατρέπει τις δύο ποσότητες από την αφαίρεση της φάσης στην πρόσθεση. Το διάγραμμα ποσότητας φάσης φαίνεται στο Σχήμα 4.
Σχήμα 4 Αρχή της μεθόδου πρόσθεσης φάσεων για τον υπολογισμό της διαφοράς φάσης
Μια άλλη βελτιωμένη μέθοδος δεν χρησιμοποιεί την διαίρεση συχνότητας σήματος ορθογώνιας κυματομορφής τάσης, αλλά χρησιμοποιεί έναν μικροϋπολογιστή για την ταυτόχρονη καταγραφή της κυματομορφής σήματος, αντίστοιχα, μέσω της διεπαφής εισόδου, καταγράφει τις κυματομορφές σήματος τάσης χωρίς φορτίο και θέσης ρότορα U0, E0, καθώς και τα ορθογώνια σήματα κυματομορφής τάσης φορτίου και θέσης ρότορα U1, E1, και στη συνέχεια μετακινεί τις κυματομορφές των δύο εγγραφών μεταξύ τους μέχρι οι κυματομορφές δύο ορθογώνιων σημάτων τάσης να επικαλύπτονται πλήρως, όταν η διαφορά φάσης μεταξύ των δύο σημάτων θέσης ρότορα είναι η γωνία ισχύος. Ή μετακινεί την κυματομορφή ώστε οι δύο κυματομορφές σήματος θέσης ρότορα να συμπίπτουν, τότε η διαφορά φάσης μεταξύ των δύο σημάτων τάσης είναι η γωνία ισχύος.
Πρέπει να επισημανθεί ότι κατά την πραγματική λειτουργία χωρίς φορτίο ενός σύγχρονου κινητήρα μόνιμου μαγνήτη, η γωνία ισχύος δεν είναι μηδέν, ειδικά για μικρούς κινητήρες. Λόγω της λειτουργίας χωρίς φορτίο, οι απώλειες χωρίς φορτίο (συμπεριλαμβανομένης της απώλειας χαλκού στον στάτορα, της απώλειας σιδήρου, της μηχανικής απώλειας, της απώλειας αδέσποτων) είναι σχετικά μεγάλες. Αν θεωρήσετε ότι η γωνία ισχύος χωρίς φορτίο είναι μηδέν, θα προκληθεί μεγάλο σφάλμα στη μέτρηση της γωνίας ισχύος, το οποίο μπορεί να χρησιμοποιηθεί για να κάνει τον κινητήρα συνεχούς ρεύματος να λειτουργεί στην κατάσταση του κινητήρα, την κατεύθυνση του τιμονιού και το τιμόνι του κινητήρα δοκιμής συνεπή. Με το τιμόνι του κινητήρα συνεχούς ρεύματος, ο κινητήρας συνεχούς ρεύματος μπορεί να λειτουργεί στην ίδια κατάσταση και ο κινητήρας συνεχούς ρεύματος μπορεί να χρησιμοποιηθεί ως κινητήρας δοκιμής. Αυτό μπορεί να κάνει τον κινητήρα συνεχούς ρεύματος να λειτουργεί στην κατάσταση του κινητήρα, το τιμόνι και το τιμόνι του κινητήρα δοκιμής συνεπή με τον κινητήρα συνεχούς ρεύματος για να παρέχει όλες τις απώλειες άξονα του κινητήρα δοκιμής (συμπεριλαμβανομένης της απώλειας σιδήρου, της μηχανικής απώλειας, της απώλειας αδέσποτων κ.λπ.). Η μέθοδος κρίσης είναι ότι η ισχύς εισόδου του κινητήρα δοκιμής είναι ίση με την κατανάλωση χαλκού του στάτορα, δηλαδή P1 = pCu, και η τάση και το ρεύμα σε φάση. Αυτή τη φορά η μετρούμενη θ1 αντιστοιχεί στη μηδενική γωνία ισχύος.
Σύνοψη: Τα πλεονεκτήματα αυτής της μεθόδου:
① Η μέθοδος άμεσου φορτίου μπορεί να μετρήσει την επαγωγή κορεσμού σταθερής κατάστασης υπό διάφορες καταστάσεις φορτίου και δεν απαιτεί στρατηγική ελέγχου, η οποία είναι διαισθητική και απλή.
Επειδή η μέτρηση γίνεται απευθείας υπό φορτίο, μπορούν να ληφθούν υπόψη το φαινόμενο κορεσμού και η επίδραση του ρεύματος απομαγνήτισης στις παραμέτρους επαγωγής.
Μειονεκτήματα αυτής της μεθόδου:
① Η μέθοδος άμεσου φορτίου πρέπει να μετρά περισσότερες ποσότητες ταυτόχρονα (τριφασική τάση, τριφασικό ρεύμα, γωνία συντελεστή ισχύος κ.λπ.), η μέτρηση της γωνίας ισχύος είναι πιο δύσκολη και η ακρίβεια της δοκιμής κάθε ποσότητας έχει άμεσο αντίκτυπο στην ακρίβεια των υπολογισμών των παραμέτρων και είναι εύκολο να συσσωρευτούν όλα τα είδη σφαλμάτων στη δοκιμή παραμέτρων. Επομένως, όταν χρησιμοποιείται η μέθοδος άμεσου φορτίου για τη μέτρηση των παραμέτρων, πρέπει να δοθεί προσοχή στην ανάλυση σφαλμάτων και να επιλεγεί υψηλότερη ακρίβεια του οργάνου δοκιμής.
② Η τιμή της ηλεκτροκινητικής δύναμης διέγερσης E0 σε αυτήν τη μέθοδο μέτρησης αντικαθίσταται απευθείας από την τάση του ακροδέκτη του κινητήρα χωρίς φορτίο, και αυτή η προσέγγιση φέρνει επίσης εγγενή σφάλματα. Επειδή, το σημείο λειτουργίας του μόνιμου μαγνήτη αλλάζει με το φορτίο, πράγμα που σημαίνει ότι σε διαφορετικά ρεύματα στάτορα, η διαπερατότητα και η πυκνότητα ροής του μόνιμου μαγνήτη είναι διαφορετικές, επομένως η προκύπτουσα ηλεκτροκινητική δύναμη διέγερσης είναι επίσης διαφορετική. Με αυτόν τον τρόπο, δεν είναι πολύ ακριβές να αντικατασταθεί η ηλεκτροκινητική δύναμη διέγερσης υπό συνθήκες φορτίου με την ηλεκτροκινητική δύναμη διέγερσης χωρίς φορτίο.
Αναφορές
[1] Tang Renyuan et al. Σύγχρονη θεωρία και σχεδιασμός κινητήρων μόνιμου μαγνήτη. Πεκίνο: Machinery Industry Press. Μάρτιος 2011
[2] JF Gieras, M. Wing. Τεχνολογία, Σχεδιασμός και Εφαρμογές Κινητήρων Μόνιμου Μαγνήτη, 2η έκδοση. Νέα Υόρκη: Marcel Dekker, 2002:170~171
Πνευματικά δικαιώματα: Αυτό το άρθρο είναι μια ανατύπωση του δημόσιου αριθμού WeChat motor peek (电机极客), του αρχικού συνδέσμουhttps://mp.weixin.qq.com/s/Swb2QnApcCWgbLlt9jMp0A
Αυτό το άρθρο δεν αντιπροσωπεύει τις απόψεις της εταιρείας μας. Εάν έχετε διαφορετικές γνώμες ή απόψεις, παρακαλούμε διορθώστε μας!
Ώρα δημοσίευσης: 18 Ιουλίου 2024